ACADEMIA DE CIENCIAS

En esta sección, exploraremos de manera simple y práctica el conjunto de los números naturales, introduciéndonos gradualmente en el fascinante mundo de las Matemáticas.
En matemáticas, los números naturales son aquellos que se utilizan para contar y ordenar elementos en conjuntos finitos, así como también para representar la posición en una secuencia o enumerar eventos. Este conjunto de números comienzan desde el 1 y se extienden hasta el infinito. Se representan con el símbolo ℕ= {1, 2, 3, 4, …} y son uno de los conceptos fundamentales en matemáticas desde la aritmética básica hasta teoría de números y más allá.
Los números naturales, son los primeros que aprendemos en nuestra infancia y siguen siendo una parte esencial de nuestro día a día, además nos permiten responder preguntas simples pero importantes, como por ejemplo:
Este conjunto de números son la base sobre la cual construimos conceptos más complejos en matemáticas, como los números enteros, racionales, irracionales y reales.
Una de las características más interesantes de los números naturales es que forman un conjunto infinito, no importa cuántos números naturales enumeremos, siempre habrá uno más. Esta propiedad ilustra la riqueza y la infinitud del mundo matemático.
OPERACIONES BÁSICAS
Los números naturales nos ofrecen, la base para realizar una variedad de operaciones fundamentales como sumar, restar, multiplicar y dividir, las cuales brindan una base sólida para abordar conceptos más avanzados en las matemáticas. A continuación, se desarrollarán de forma simple los conceptos de esta operaciones:
SUMA:
La suma de números naturales es una operación básica en matemáticas que consiste en combinar dos o más números para obtener un total. En una suma, hay varias partes que podemos identificar:
- Sumandos: Son los números que se están sumando entre sí.
- Signo de Suma: Es el símbolo «+» que indica la operación de suma entre los sumandos.
- Resultado o Total: Es el número obtenido al combinar los sumandos.
Para realizar una suma, simplemente agregamos los números entre sí. A continuación se refleja un ejemplo:

RESTA:
La resta de números naturales es una operación matemática básica que consiste en encontrar la diferencia entre dos cantidades. En la resta hay varias partes que podemos identificar:
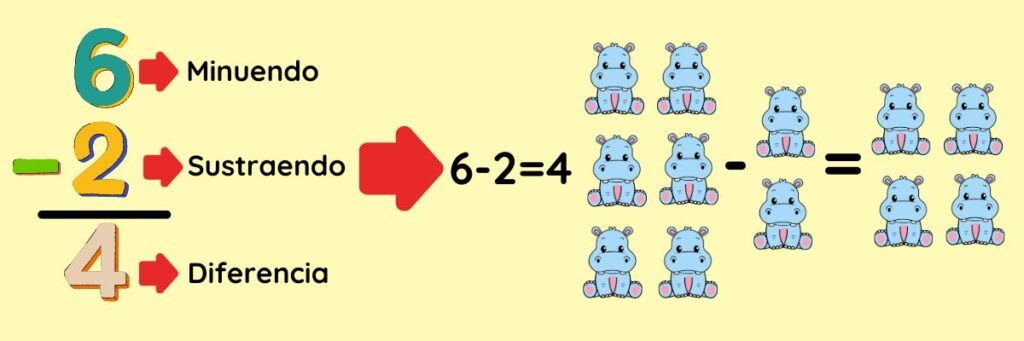
- Minuendo: Es el número más grande en una operación, del cual se resta otro número.
- Sustraendo: Es el número más pequeño en una operación y el cual se «sustrae» o resta del minuendo.
- Diferencia: Es el resultado de la resta.
Para realizar una resta, colocamos el número más grande (el minuendo) en la parte superior y el número más pequeño (el sustraendo) debajo, como se muestra a continuación:
MULTIPLICACIÓN:
La multiplicación de números naturales es una operación fundamental en matemáticas que consiste en sumar repetidamente un número determinado de veces. En la multiplicación hay varias partes que podemos identificar:
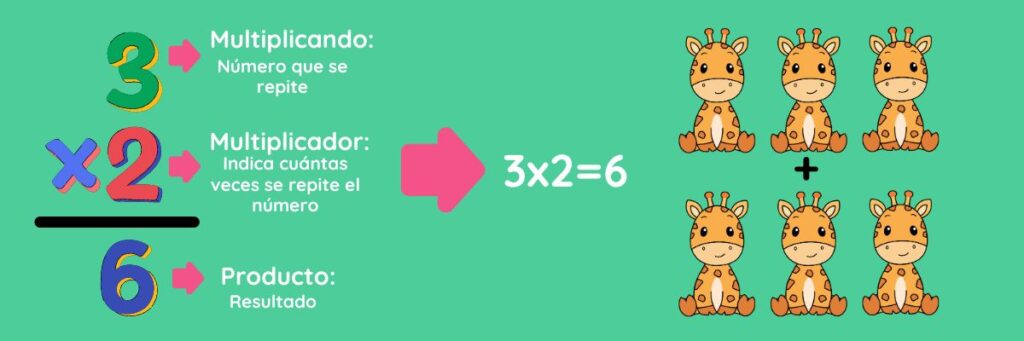
- Multiplicando: Es el número que se multiplica por otro número. Es el primer factor en una operación de multiplicación.
- Multiplicador: Es el número que indica cuántas veces se repite o se suma el multiplicando. Es el segundo factor en una operación de multiplicación.
- Producto: Es el resultado de la multiplicación.
Para realizar ésta operación, se multiplican los números llamados multiplicando y multiplicador, tal como se muestra en la figura:
Procedimiento:
Es crucial comprender el proceso de la multiplicación para resolver problemas matemáticos y comprender las relaciones numéricas. Por esta razón, a continuación, presentaremos el procedimiento detallado de la multiplicación de 89×7:
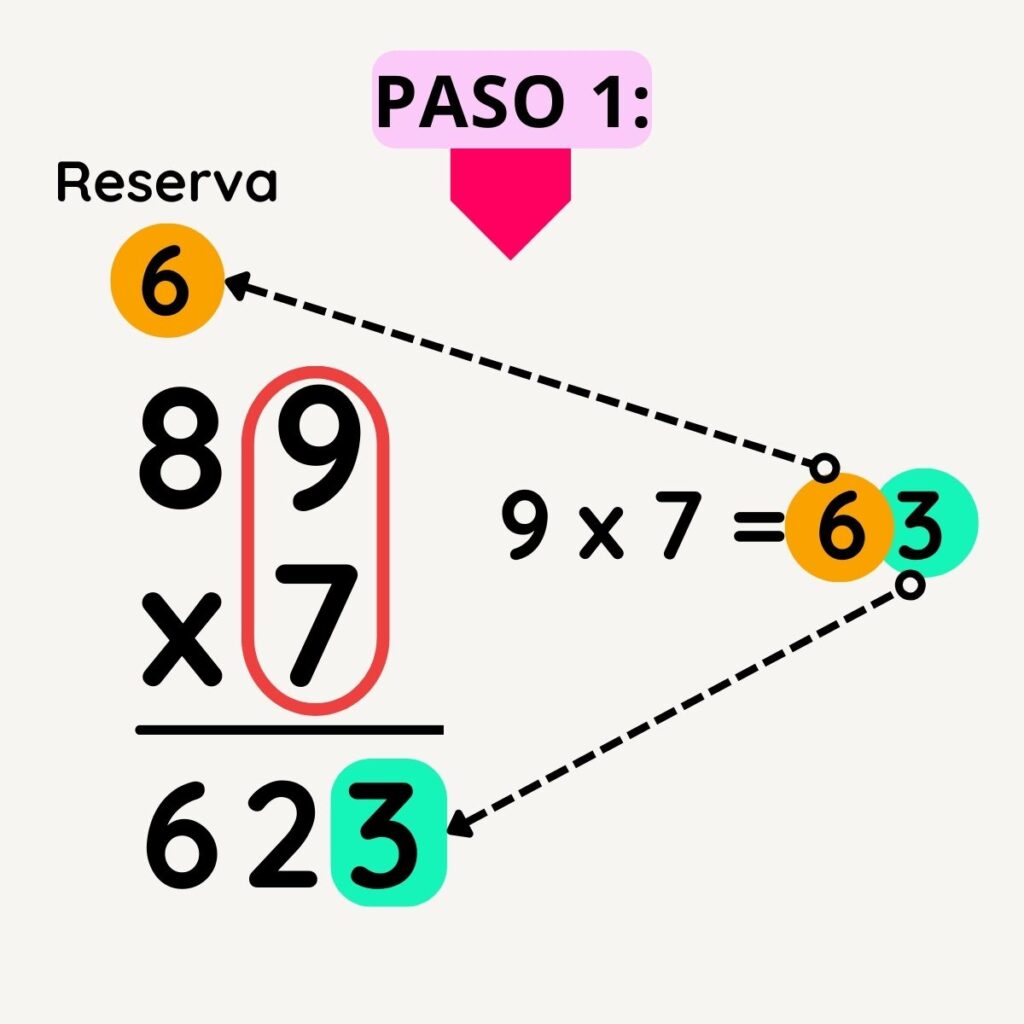
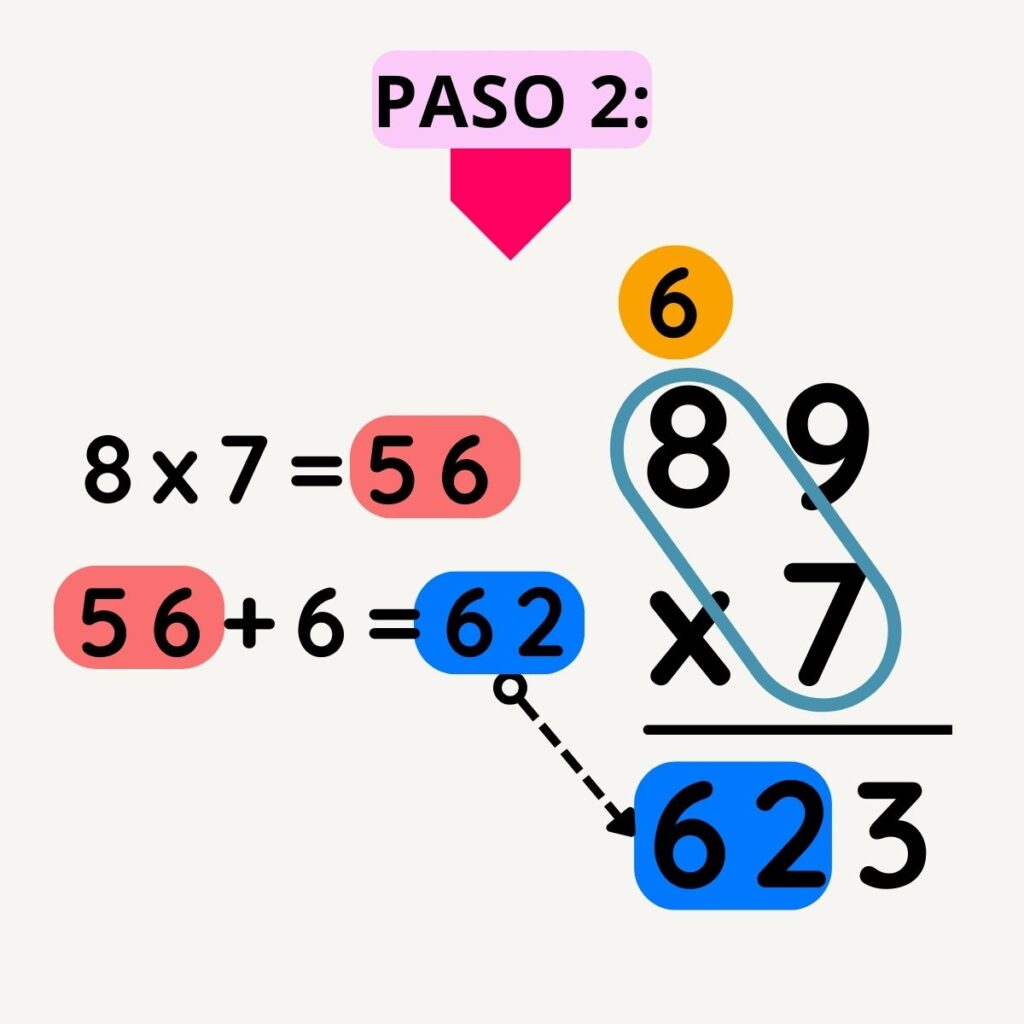
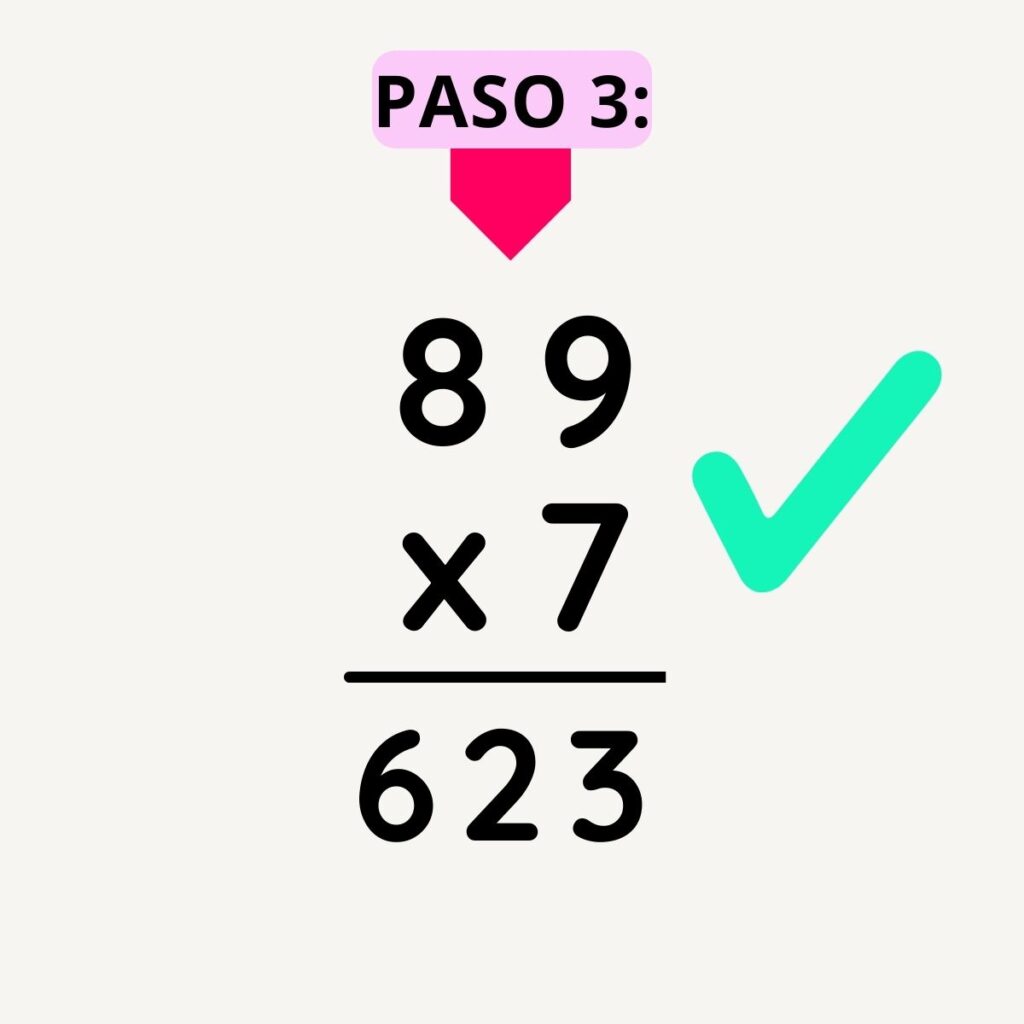
Fig.5. Procedimiento para multiplicar
DIVISIÓN:
La división de números naturales es una operación matemática fundamental que consiste en repartir o distribuir una cantidad en partes iguales. En la división hay varias partes que podemos identificar:
- Dividendo: Es el número total o la cantidad que se divide en partes iguales.
- Divisor: Es el número que indica en cuántas partes se divide el dividendo.
- Cociente: Es el resultado de la división.
- Residuo: Es la cantidad sobrante después de realizar la división. Si no hay un residuo, la división es exacta y si al final de la operación resultó un número distinto de cero, la división es considerada inexacta.
Para realizar una división, se utilizan dos números: el dividendo y el divisor. A continuación se presenta un esquema de como funciona la división:
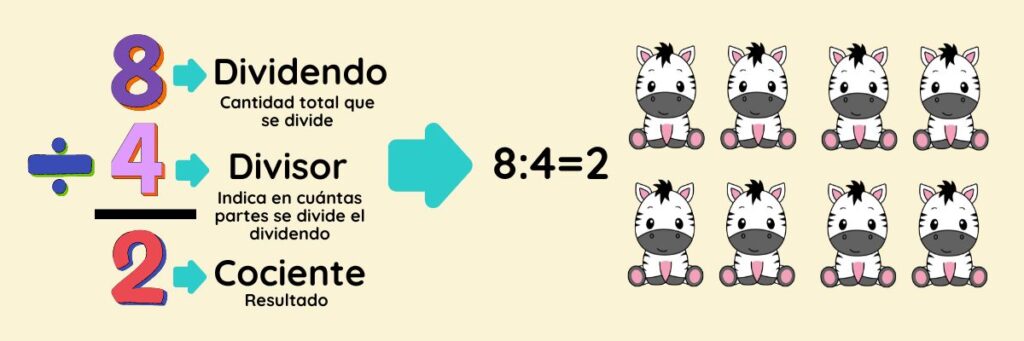
Procedimiento:
Aprender a dividir es fundamental por varias razones. Primero, la división nos permite distribuir cantidades en partes iguales, lo que es esencial en numerosas situaciones de la vida diaria, como dividir alimentos, repartir dinero o calcular la duración de un viaje. Además, la división nos ayuda a comprender la relación entre diferentes cantidades y a resolver problemas matemáticos más complejos.
Dominar la división también es crucial para comprender conceptos matemáticos avanzados, como fracciones, porcentajes y proporciones. En resumen, aprender a dividir nos proporciona habilidades prácticas y conceptuales que son esenciales para el éxito en matemáticas y en la vida cotidiana. Por tales motivos, describiremos el procedimiento de la división de forma detallada:
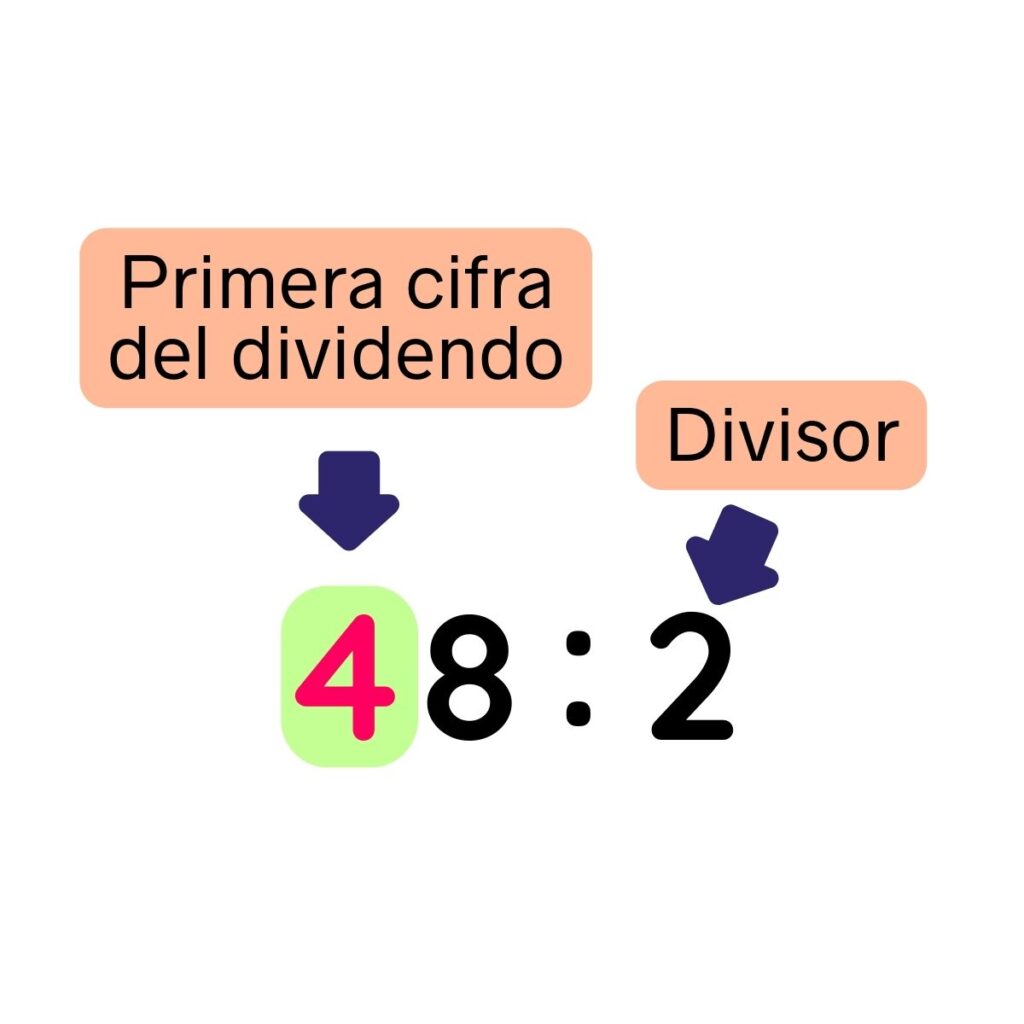
PASO 1: Comienza dividiendo la primera cifra del dividendo (4) entre el divisor (2).
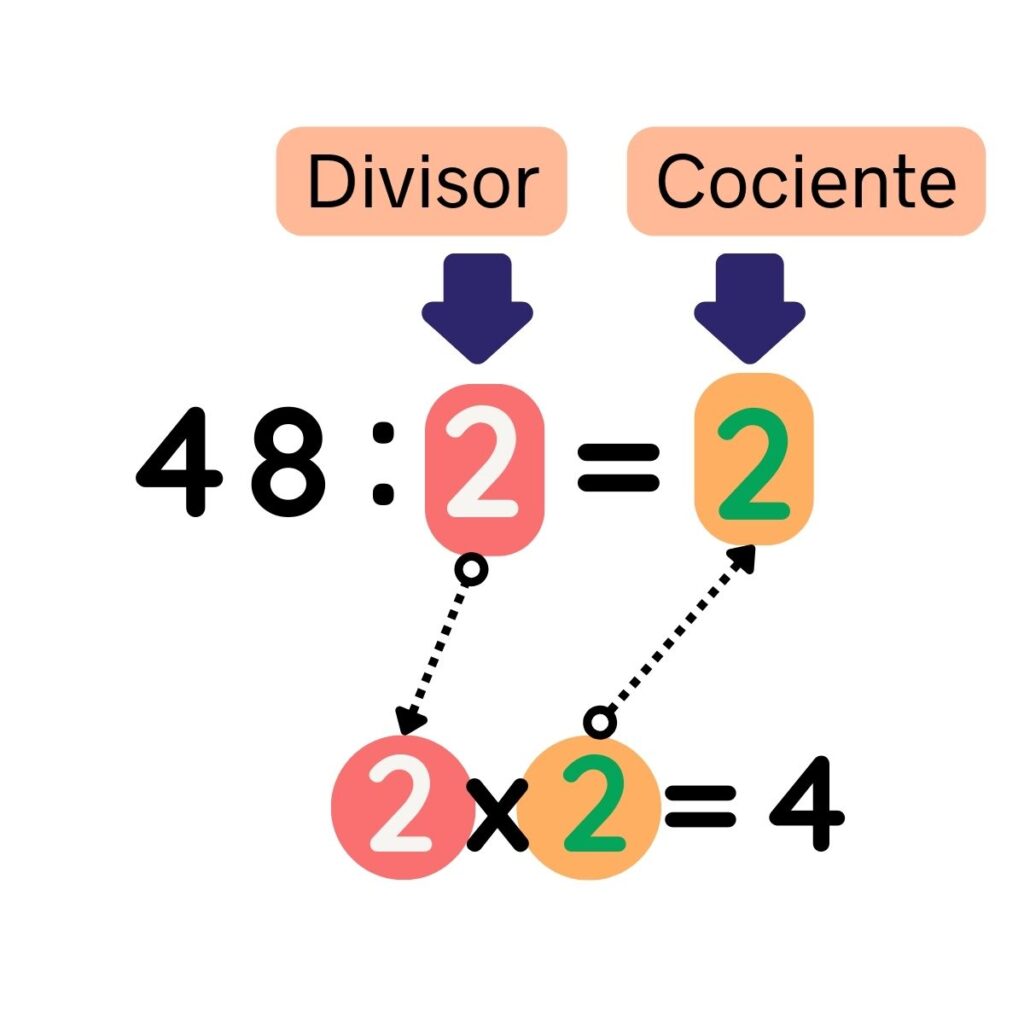
PASO 2: Buscar un número que multiplicado por el divisor (2), resulte un número igual o cercano al dividendo (4) y colocar el número en el cociente. El número es el 2.
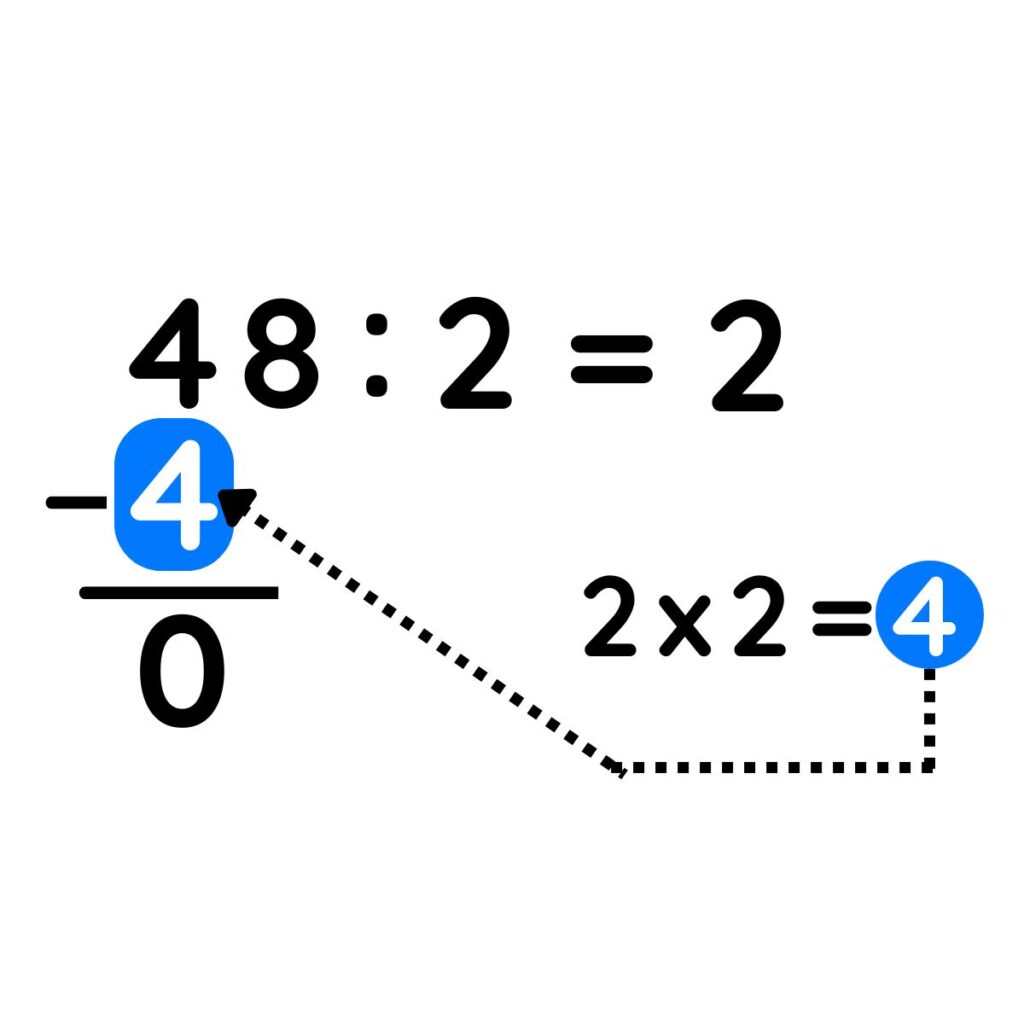
PASO 3: Colocar el resultado de la multiplicación (4), debajo de la primera cifra del dividendo (4) y restar. El resultado es cero.
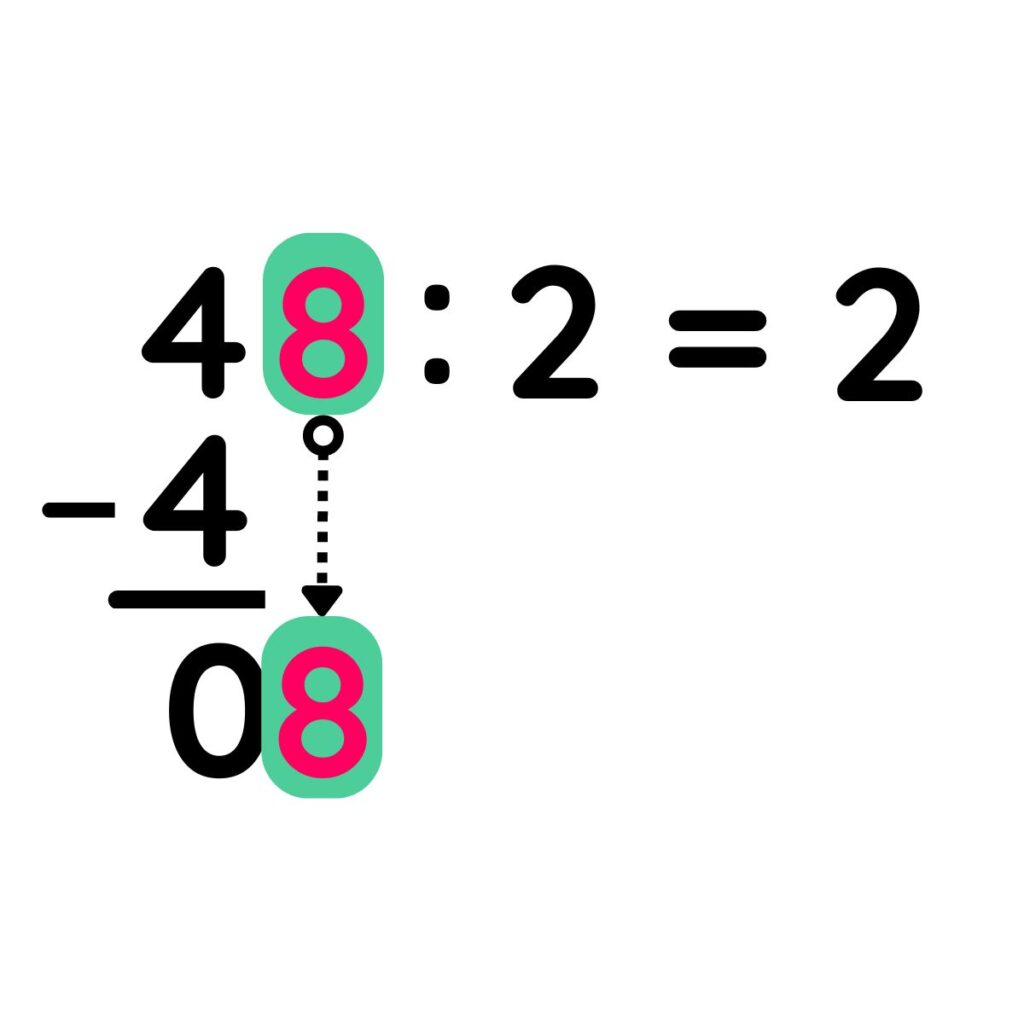
PASO 4: Después de restar, seleccionar la siguiente cifra del dividendo (8) y bajarla.
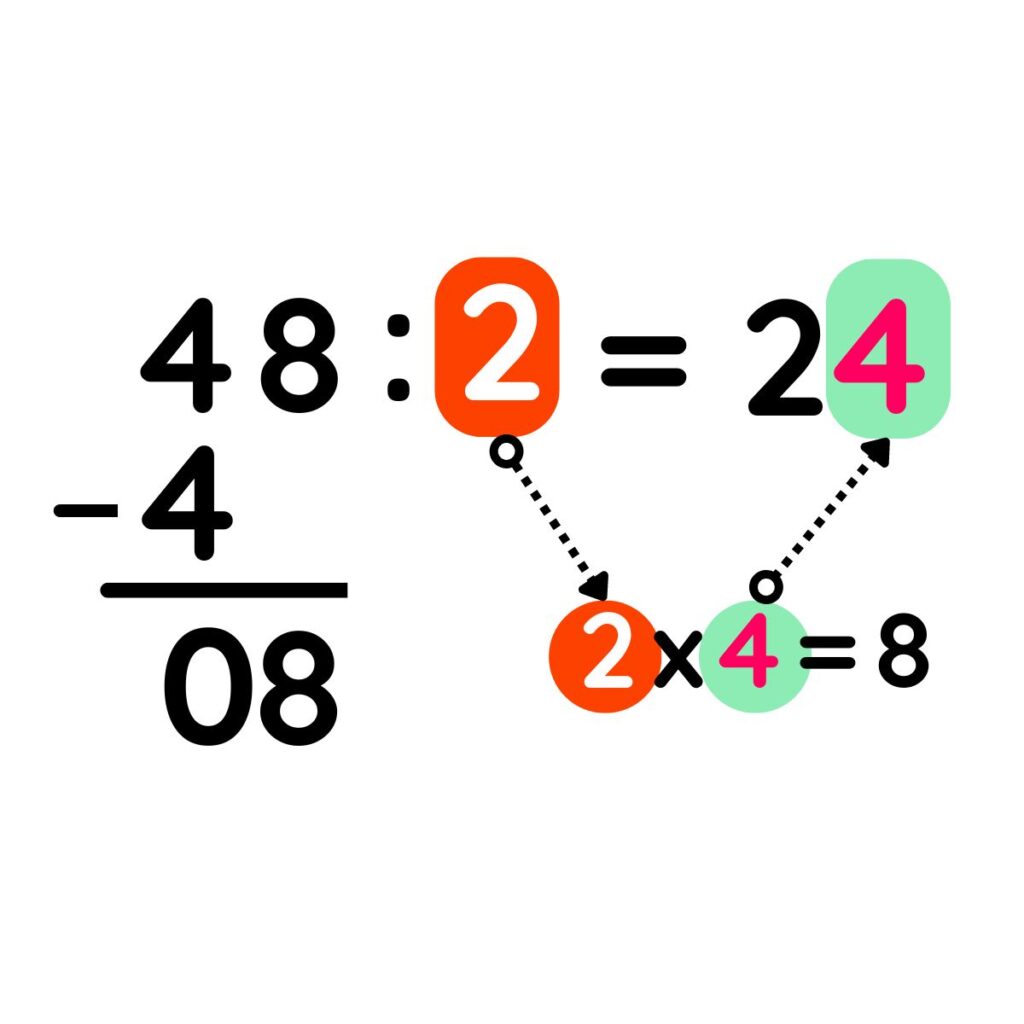
PASO 5: Repetir el paso 2, buscar un número que multiplicado por el divisor (2), resulte un número igual o cercano a 8 y colocar en el cociente. El número es el 4.
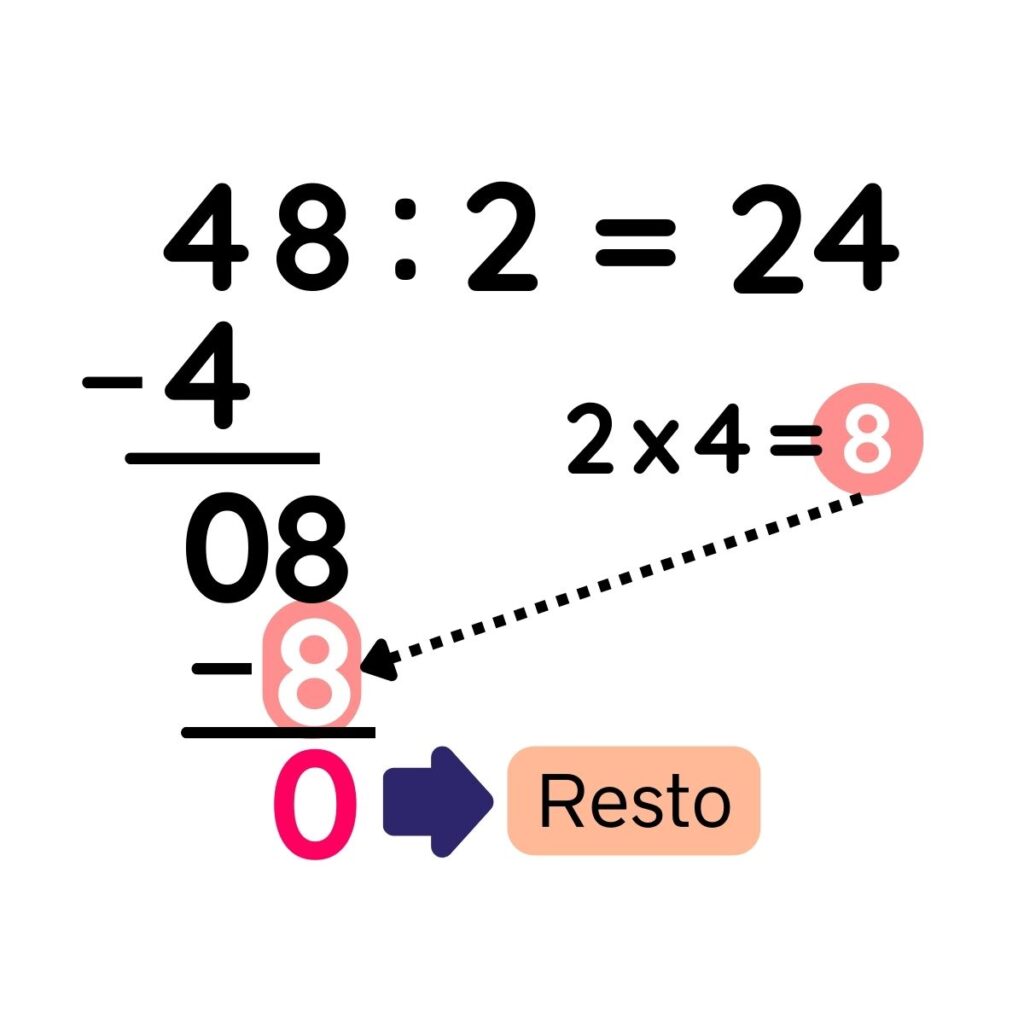
PASO 6: Colocar el resultado (8) debajo de la segunda cifra del dividendo (8) y restar, obteniendo un resto igual a cero. Por lo tanto, esta división es exacta.
Fig.7.Procedimiento para dividir
En resumen, los números naturales y sus operaciones son fundamentales en matemáticas y en nuestra vida diaria. Son la base sobre la cual construimos nuestro entendimiento del mundo cuantitativo que nos rodea. Las operaciones como la suma, resta, multiplicación y división nos permiten resolver problemas prácticos y comprender la relación entre cantidades. Además, dominar estas operaciones es crucial para abordar conceptos matemáticos más avanzados y para desarrollar habilidades analíticas y de resolución de problemas. En conclusión, los números naturales y sus operaciones son esenciales para nuestro desarrollo matemático y el funcionamiento de nuestra sociedad en general. Es por eso que es importante comprender su importancia y practicar estas habilidades para alcanzar el éxito académico y personal.
En el siguiente artículo, desarrollaremos la segunda parte del conjunto de los números naturales.


