ACADEMIA DE CIENCIAS
En esta publicación, exploraremos el intrigante mundo de los conjuntos numéricos, fundamentales en matemáticas para dominar el álgebra y el cálculo. Nuestro objetivo es comprender de manera sencilla su formación y funcionamiento en nuestra vida cotidiana y el mundo.
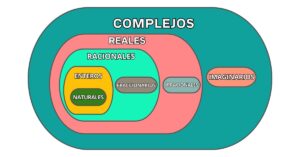
Los conjuntos numéricos en matemáticas consisten en agrupaciones de números que comparten características similares, tales como los naturales, enteros, racionales, irracionales y reales. Estos conjuntos desempeñan un papel fundamental en la clasificación y organización de los números según sus propiedades. La figura adjunta muestra el inicio de esta clasificación:
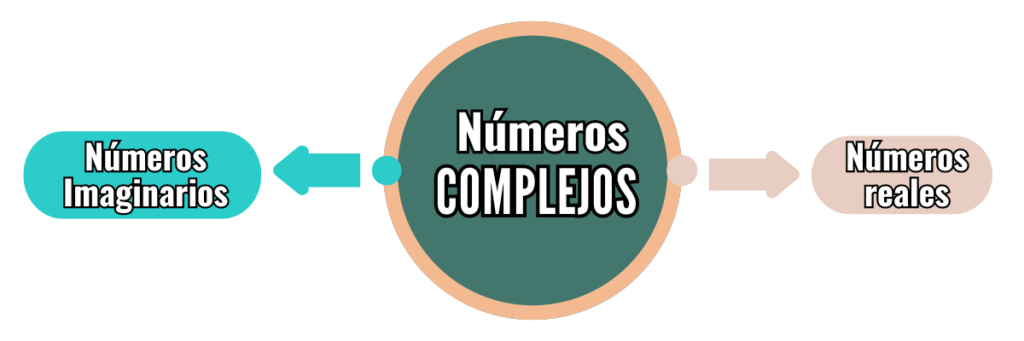
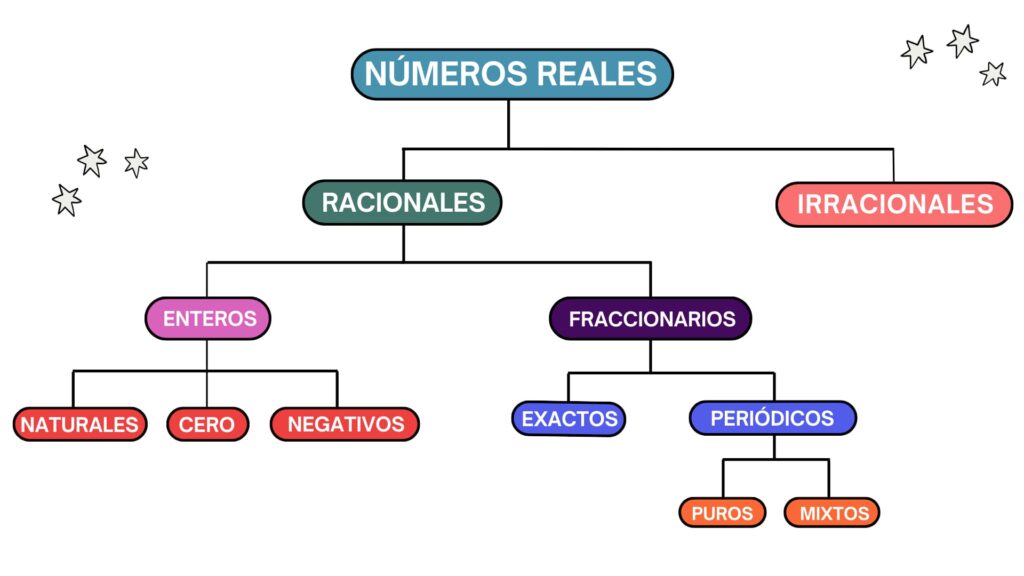
Los números complejos se dividen en dos categorías: los números reales y los imaginarios. Los números reales son los más comunes en nuestra vida cotidiana y se subdividen de la siguiente manera:
A.- Representación simbólica de los conjuntos numéricos
La representación simbólica de los conjuntos numéricos es fundamental en el ámbito matemático para expresar de manera compacta y precisa las distintas categorías de números. A través de símbolos y notaciones específicas, se puede distinguir entre conjuntos como los números naturales, enteros, racionales, irracionales y reales, cada uno con propiedades y características únicas. Esta representación simbólica no solo simplifica la comunicación matemática, sino que también facilita el análisis y la comprensión de conceptos fundamentales en diversas ramas de las matemáticas y ciencias aplicadas. En este contexto, exploraremos cómo estos símbolos nos permiten categorizar y comprender la riqueza y la diversidad de los números que nos rodean.
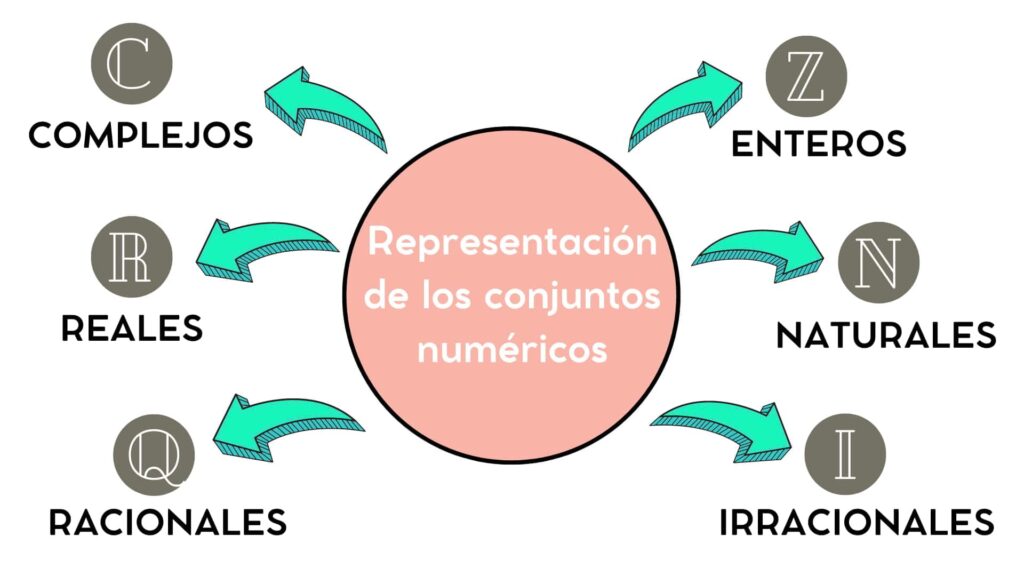
Es fundamental comprender la representación de cada conjunto para poder utilizarlos de manera efectiva. Para facilitar la comprensión de manera simple y práctica, procederemos a desarrollar cada uno de estos conjuntos a continuación:
1.- Números complejos
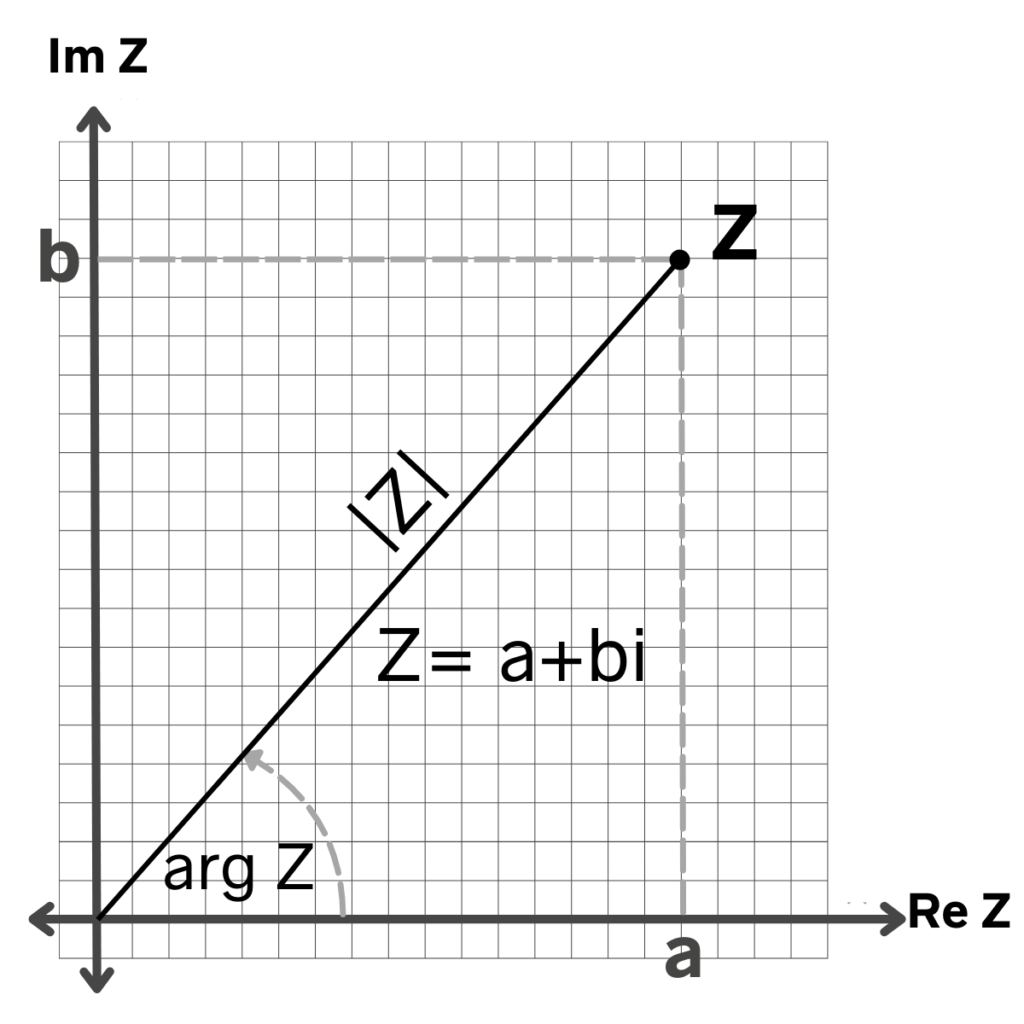
Los números complejos se extienden más allá de los números reales y se expresan como la suma de una parte real y otra imaginaria, la cual se representa como: Z=a+bi, correspondiente a su forma binómica. Son una herramienta fundamental en álgebra, análisis y diversas ramas de las matemáticas, tanto puras como aplicadas, como la variable compleja y las ecuaciones diferenciales.
Aplicación:
Los números complejos, aunque abstractos, tienen aplicaciones prácticas en diversos campos de la vida real:
- Electrónica y telecomunicaciones: En ingeniería eléctrica y electrónica, los números complejos se utilizan para representar corrientes y voltajes en circuitos eléctricos, así como para analizar señales de comunicación, como las ondas electromagnéticas.
- Mecánica cuántica: En física, los números complejos son fundamentales para describir el comportamiento de partículas subatómicas, como electrones y fotones, y los fenómenos cuánticos que rigen el mundo a escala microscópica.
- Análisis de señales y procesamiento de imágenes: En campos como la ingeniería de señales y el procesamiento de imágenes, los números complejos se utilizan para representar y manipular señales y datos, como en la compresión de imágenes digitales o en la filtración de señales de audio.
- Aerodinámica e hidrodinámica: En la ingeniería aeroespacial y la ingeniería naval, los números complejos se utilizan para modelar y simular el flujo de fluidos alrededor de objetos, como aviones, barcos y automóviles, lo que permite diseñar formas eficientes y aerodinámicas.
- Circuitos eléctricos y electrónicos: En el diseño y análisis de circuitos eléctricos y electrónicos, los números complejos se utilizan para calcular impedancias, corrientes y voltajes en sistemas de corriente alterna, lo que permite optimizar el rendimiento y la eficiencia de los dispositivos electrónicos.
En resumen, los números complejos son una herramienta poderosa y versátil que se utiliza en una amplia gama de campos, desde la ingeniería y la física hasta la tecnología y la ciencia de datos, contribuyendo al desarrollo y avance de la sociedad moderna.
2.- Números reales
Los números reales constituyen un conjunto que abarca tanto los números racionales como los irracionales. Esto incluye a los números enteros, fraccionarios y decimales, así como también números como π y √2, que no pueden ser expresados como una fracción simple. En esencia, los números reales son aquellos que se pueden encontrar en la línea numérica, abarcando todas las magnitudes posibles, tanto positivas como negativas.

Aplicación:
Los números reales son omnipresentes en la vida cotidiana y se utilizan en una variedad de contextos, por lo que se muestra algunas de sus aplicaciones:
- Finanzas personales y comerciales: Los números reales se utilizan para representar valores monetarios, como precios, ingresos, gastos y balances bancarios. Ya sea al comprar comestibles, pagar facturas o calcular ganancias empresariales, los números reales son esenciales en transacciones financieras.
- Medidas y dimensiones: Los números reales se utilizan para medir longitudes, áreas, volúmenes, pesos, velocidades y otras magnitudes físicas. Por ejemplo, las distancias de viaje, las dimensiones de una casa o el peso de un objeto se expresan en números reales.
- Temperaturas: Los números reales se usan para medir temperaturas en grados Celsius o Fahrenheit. Ya sea para vestirse adecuadamente para el clima, ajustar la calefacción del hogar o monitorear la temperatura de los alimentos, los números reales son esenciales en la vida diaria.
- Tiempo: Los números reales se utilizan para medir el tiempo en horas, minutos y segundos. Desde planificar horarios y citas hasta programar actividades diarias, los números reales son fundamentales en la organización del tiempo.
- Puntuaciones y calificaciones: Los números reales se utilizan para representar puntuaciones en exámenes, calificaciones escolares, clasificaciones deportivas y evaluaciones laborales. Estas puntuaciones influyen en decisiones importantes, como la admisión a instituciones educativas o la contratación laboral.
En resumen, los números reales son esenciales en la vida cotidiana y se utilizan en una variedad de situaciones para representar cantidades, mediciones, valores monetarios, temperaturas, tiempo y evaluaciones, entre otros aspectos de la experiencia humana.
3.- Números racionales
Los números racionales son aquellos que pueden expresarse como el cociente de dos números enteros, donde el denominador no es igual a cero. En otras palabras, son todos aquellos números que pueden ser escritos en forma de fracción, donde el numerador y el denominador son enteros. Esto incluye tanto a los números enteros como a los fraccionarios. Por ejemplo, 1/2, -3/4, 5/1, y -7 son todos números racionales. Los números racionales son fundamentales en matemáticas y se utilizan en una variedad de contextos, desde operaciones aritméticas básicas hasta la resolución de ecuaciones y problemas en la vida cotidiana.
Aplicación:
A continuación se muestran algunas situaciones comunes en las que se usan este conjunto de números:
- Mediciones y cantidades fraccionarias: Desde dividir una pizza entre amigos hasta calcular la cantidad de tela necesaria para cortinas; los números racionales nos permiten expresar fracciones de cantidades de manera precisa.
- Finanzas personales: En el ámbito financiero, los números racionales son esenciales para calcular porcentajes, tasas de interés y realizar operaciones con dinero, como dividir cuentas o calcular descuentos.
- Cocina y recetas: Muchas recetas requieren medidas fraccionarias, como 1/4 de taza de harina o 3/4 de cucharadita de sal, lo que implica el uso de números racionales para lograr las proporciones adecuadas.
- Tiempo y velocidad: Cuando medimos el tiempo en fracciones de horas, como 1/2 hora o 3/4 hora, o calculamos velocidades medias en kilómetros por hora, estamos usando números racionales.
- Construcción y carpintería: En proyectos de construcción y carpintería, las mediciones de longitud y área suelen expresarse en fracciones, como 1/2 pulgada o 2 1/4 pies, lo que implica el uso de números racionales.
En resumen, los números racionales son fundamentales en muchas áreas de la vida cotidiana donde se requiere precisión en las mediciones, cálculos de proporciones y divisiones de cantidades.
4.- Números irracionales
Los números irracionales son aquellos números reales que no pueden expresarse como el cociente de dos números enteros. En otras palabras, no pueden ser representados de manera exacta por una fracción. Su representación decimal es no periódica y no termina nunca. Ejemplos clásicos de números irracionales incluyen π (pi), √2 (raíz cuadrada de 2), e (número de Euler) y φ (número áureo). Estos números tienen infinitos dígitos decimales no repetitivos, lo que los hace difíciles de representar de manera exacta. A pesar de esto, los números irracionales son fundamentales en matemáticas y se utilizan en diversos contextos, como geometría, física, estadística y cálculo avanzado.

Fig. 7. Números irracionales
Los números irracionales, aunque menos evidentes en su uso directo en la vida diaria que los números enteros o naturales, tienen aplicaciones importantes en diversas áreas:
- Geometría: Muchas medidas en geometría involucran números irracionales, como la longitud de una diagonal de un cuadrado de lado 1 (raíz cuadrada de 2) o el radio de un círculo (π). Estos números son fundamentales para calcular áreas, volúmenes y otras propiedades geométricas.
- Ciencias naturales: En física, la constante π aparece en fórmulas que describen fenómenos naturales, como la circunferencia de un círculo o la frecuencia de oscilación de una onda. También se utiliza en la ingeniería para diseñar estructuras y dispositivos.
- Finanzas: Los números irracionales a menudo se utilizan en cálculos financieros, como en el cálculo de tasas de interés compuesto o la valoración de inversiones a largo plazo.
- Tecnología: En campos como la informática y la ingeniería de software, los números irracionales se utilizan en algoritmos y cálculos numéricos avanzados para modelar y simular sistemas complejos.
- Arte y diseño: Los números irracionales también tienen aplicaciones en el arte y el diseño, donde se utilizan para crear patrones geométricos, representaciones visuales de la naturaleza y formas estéticamente agradables.
En resumen, aunque los números irracionales no se utilizan directamente en muchas actividades cotidianas, tienen aplicaciones importantes en campos como la geometría, las ciencias naturales, las finanzas, la tecnología y el arte, contribuyendo al desarrollo y comprensión de diversos aspectos de nuestro mundo.
5.- Números enteros
Los números enteros son un conjunto que incluye a todos los números naturales (positivos) junto con sus respectivos opuestos negativos y el número cero. En otras palabras, los números enteros son -3, -2, -1, 0, 1, 2, 3, y así sucesivamente. Estos números se utilizan para representar tanto cantidades positivas como negativas, así como para realizar operaciones matemáticas como suma, resta, multiplicación y división. Los números enteros son fundamentales en matemáticas y se utilizan en una amplia variedad de contextos, desde contabilidad y finanzas hasta física y programación de computadoras.

Aplicación:
Los números enteros son utilizados en numerosas situaciones cotidianas para representar cantidades y realizar operaciones matemáticas. Aquí hay algunos ejemplos de cómo se usan:
- Temperaturas: Los números enteros se utilizan para medir temperaturas, tanto en grados Celsius como en grados Fahrenheit. Por ejemplo, si la temperatura es de 10 grados Celsius, se representa como +10°C, mientras que -5°C indica una temperatura bajo cero.
- Dinero: Los números enteros se usan para representar cantidades monetarias en finanzas personales y comerciales. Por ejemplo, si tienes $50 en tu billetera y gastas $20, quedas con $30.
- Edades: Los números enteros se utilizan para representar edades. Por ejemplo, si alguien tiene 25 años, se representa como el número entero 25.
- Puntos en juegos o deportes: En juegos y deportes, los números enteros se utilizan para representar puntuaciones, puntos o posiciones. Por ejemplo, si un equipo de fútbol tiene 3 puntos en una tabla de posiciones, se representa como el número entero 3.
- Distancias y posiciones: Los números enteros se utilizan para representar distancias y posiciones en navegación, geometría y otras áreas. Por ejemplo, si caminas 5 kilómetros hacia el norte, tu posición cambia en +5 kilómetros.
En resumen, los números enteros son parte integral de la vida cotidiana y se utilizan en una variedad de situaciones para representar cantidades, posiciones y valores numéricos.
6.- Números Naturales
Los números naturales son aquellos números que se utilizan para contar objetos o representar cantidades de manera no negativa. El conjunto de números naturales comienza con el número 1 y continúa indefinidamente, incluyendo todos los números enteros positivos. En otras palabras, son los números que usarías para contar cosas, como el número de manzanas en una canasta o el número de estudiantes en un aula. Los números naturales forman la base de las matemáticas básicas. Son fundamentales en una variedad de contextos, desde resolver problemas aritméticos simples hasta representar conceptos en ciencias naturales y sociales.

Aplicación:
Los números naturales son una parte fundamental de nuestra vida diaria y se utilizan en una variedad de situaciones:
- Contar objetos: Los números naturales se usan para contar objetos, como el número de manzanas en una cesta o el número de libros en una estantería.
- Edades: Se utilizan para representar la edad de las personas. Por ejemplo, si alguien tiene 30 años, se representa como el número natural 30.
- Números de teléfono: Cada vez que marcamos un número de teléfono, estamos utilizando números naturales para identificar a quién queremos llamar.
- Horario: Los números naturales se utilizan para indicar la hora en relojes analógicos y digitales. Por ejemplo, si son las 8 de la mañana, se representa como el número natural 8.
- Calendario: Se utilizan para indicar el día del mes en calendarios. Por ejemplo, si hoy es el día 15, se representa como el número natural 15.
En resumen, los números naturales son esenciales en nuestra vida diaria y se utilizan en una variedad de situaciones para contar, medir el tiempo y representar cantidades.
Hemos simplificado de manera práctica el concepto de cada conjunto numérico con el objetivo de comprender tanto sus fundamentos como su aplicación en diversas situaciones cotidianas. Además, buscamos resaltar la relevancia de cada conjunto en nuestra vida y en el progreso global.
Después de completar el desarrollo básico de los conjuntos numéricos, nos embarcamos en una nueva fase donde profundizaremos en cada uno de ellos, comenzando con los números naturales. En esta etapa, exploraremos en detalle las propiedades, operaciones y aplicaciones de este conjunto fundamental en las matemáticas. Es importante resaltar que los números naturales, son la base sobre la cual se construyen los demás conjuntos numéricos. Desde la simple contabilización de objetos hasta la representación de patrones y secuencias, los números naturales desempeñan un papel crucial en una variedad de contextos matemáticos y aplicaciones prácticas. En la próxima publicación, nos sumergiremos en el fascinante mundo de los números naturales, explorando sus propiedades únicas y su importancia en el desarrollo de conceptos más avanzados en matemáticas. ¡Acompáñanos en este viaje de descubrimiento y aprendizaje!


