ACADEMIA DE CIENCIAS

Los números enteros son un conjunto de números que incluyen todos los números naturales (0, 1, 2, 3, …), sus opuestos negativos (-1, -2, -3, …), y el cero. Este conjunto se denota generalmente por el símbolo ℤ, que proviene de la palabra alemana «Zahlen», que significa «números». A continuación se describirá todos los puntos importantes de los números enteros.
1.- REPRESENTACIÓN EN LA RECTA NUMÉRICA
Los números enteros se pueden representar en la recta numérica de la siguiente manera:
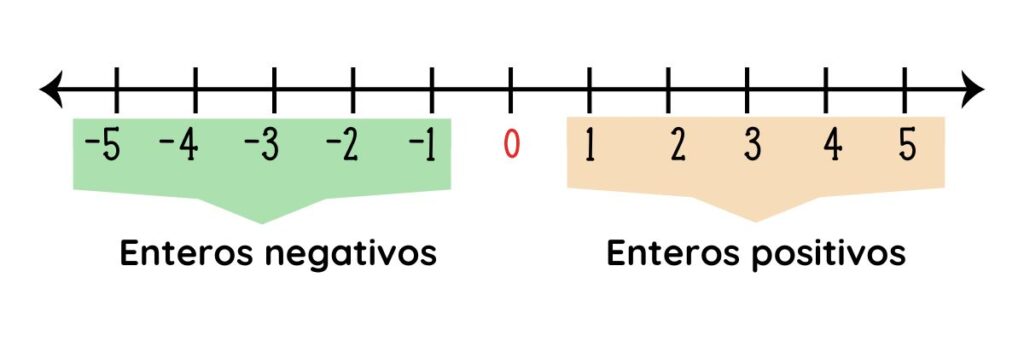
2.- CARACTERÍSTICAS PRINCIPALES
- Incluyen los números positivos y negativos: Los enteros abarcan tanto los números positivos como sus contrapartes negativas.
- Incluyen el cero: El cero es un número entero que no es ni positivo ni negativo.
- Son infinitos: No hay un número entero más grande ni uno más pequeño; se extienden infinitamente en ambas direcciones.
- Operaciones aritméticas: Se pueden realizar operaciones como la suma, resta, multiplicación y división (excepto la división por cero) con números enteros, siguiendo reglas específicas que garantizan que el resultado también sea un número entero.
3.- SIGNOS DE AGRUPACIÓN
Los signos de agrupación en matemáticas son símbolos utilizados para indicar que ciertas operaciones deben realizarse antes que otras en una expresión.
Sirven para establecer un orden específico en el que las operaciones deben ser ejecutadas, asegurando que los cálculos se realicen correctamente. Los principales signos de agrupación son:
- Paréntesis ():
- Se utilizan para agrupar términos y operaciones que deben ser realizadas primero.
- Corchetes []:
- Se utilizan cuando ya hay paréntesis en una expresión y se necesita otro nivel de agrupación.
- Llaves {}:
- Se utilizan para agrupar expresiones que ya contienen paréntesis y corchetes, proporcionando un tercer nivel de agrupación.
a) Importancia de los Signos de Agrupación:
- Claridad: Ayudan a clarificar la secuencia en la que se deben realizar las operaciones en una expresión compleja.
- Precisión: Aseguran que los cálculos se realicen correctamente, siguiendo el orden de operaciones adecuado (PEMDAS/BODMAS: Paréntesis/Brackets, Exponentes/Orders, Multiplicación y División, Adición y Sustracción).
- Desambiguación: Eliminan la ambigüedad en las expresiones matemáticas, haciendo claro qué operaciones deben ejecutarse juntas.
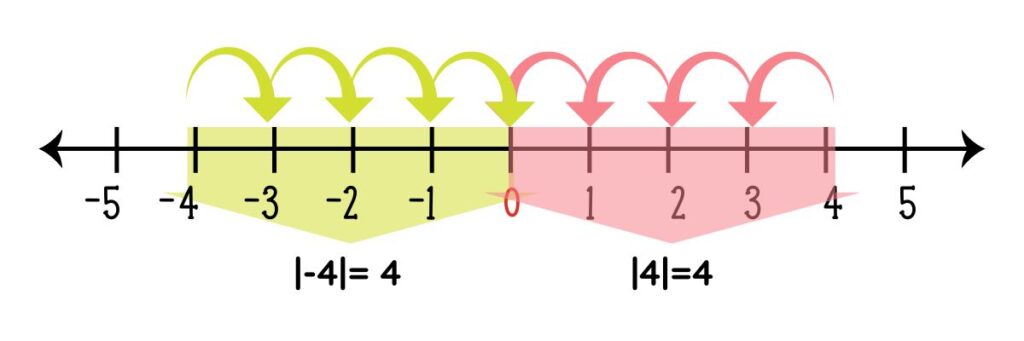
3.- VALOR ABSOLUTO
El valor absoluto es una forma de medir qué tan lejos está un número del cero en una recta numérica, sin importar si es positivo o negativo. Es como si solo miráramos la distancia sin preocuparnos de la dirección.
Por ejemplo:
- El valor absoluto de 5 es 5, porque el 5 está a 5 pasos de cero.
- El valor absoluto de -5 también es 5, porque el -5 está a 5 pasos de cero, solo que en la dirección opuesta.
Para escribir el valor absoluto de un número, usamos dos líneas verticales alrededor del número, de la siguiente manera:
- ∣5∣=5
- ∣−5∣=5
En resumen, el valor absoluto de cualquier número es siempre positivo, porque solo estamos contando los pasos hasta el cero.
4.- REGLAS Y PROPIEDADES
Existen reglas específicas para realizar las operaciones básicas con números enteros, que se describirán de manera sencilla en esta sección. Antes de iniciar con las reglas y propiedades básicas, es importante saber:

📌SUMA Y RESTA
La suma de números enteros es una operación matemática que combina dos o más enteros para formar un único entero. Dependiendo de los signos de los números involucrados (positivos o negativos), se aplican diferentes reglas para obtener el resultado.
Por su parte, la resta de números enteros es una operación matemática que encuentra la diferencia entre dos enteros. Esta operación puede ser vista como la suma del minuendo con el opuesto del sustraendo.
▶︎ REGLA DE LA SUMA
- Signos iguales se suman y se coloca el mismo signo.
- Signos diferentes se restan y se coloca el signo del número mayor. El número mayor, es aquel donde se considera solo su valor absoluto, sin tomar en cuenta el signo.
Ejemplos:
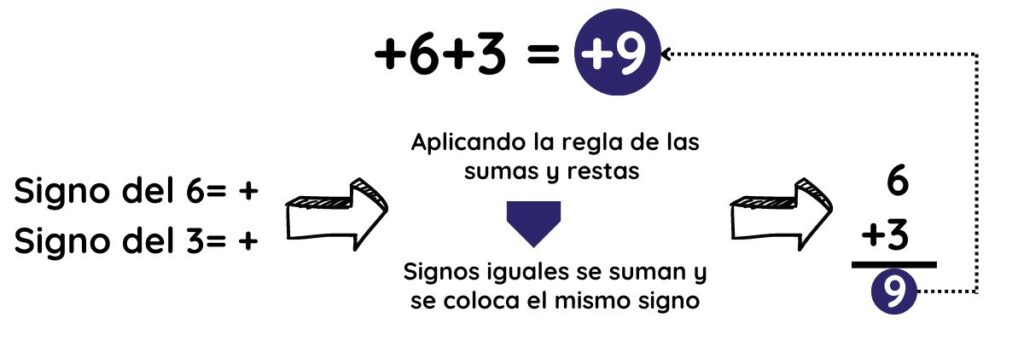
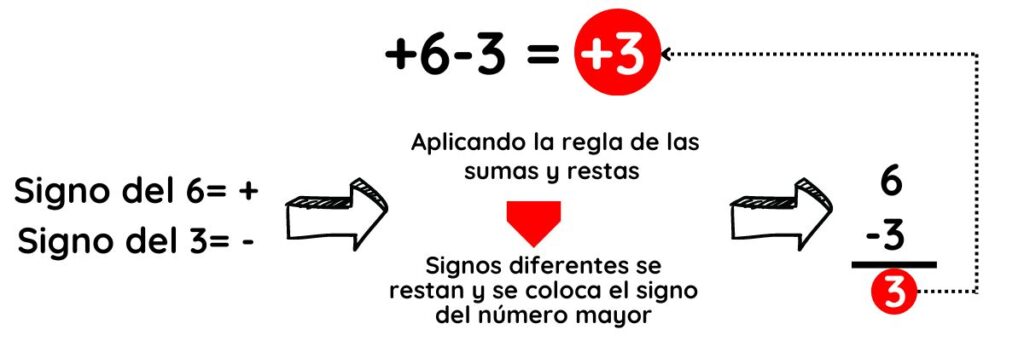
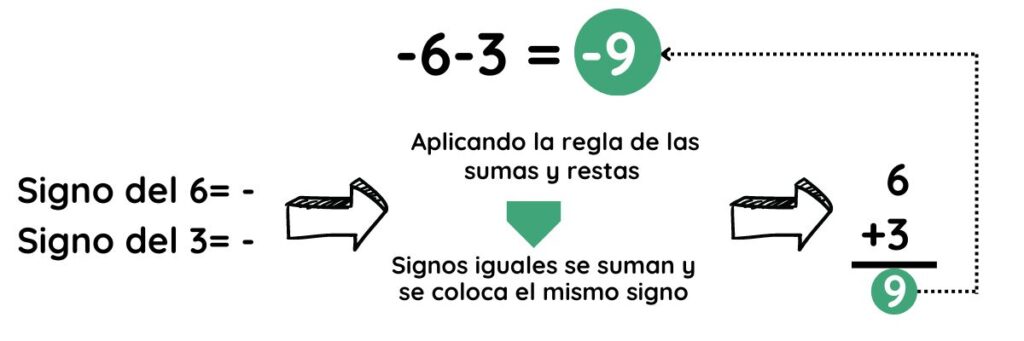
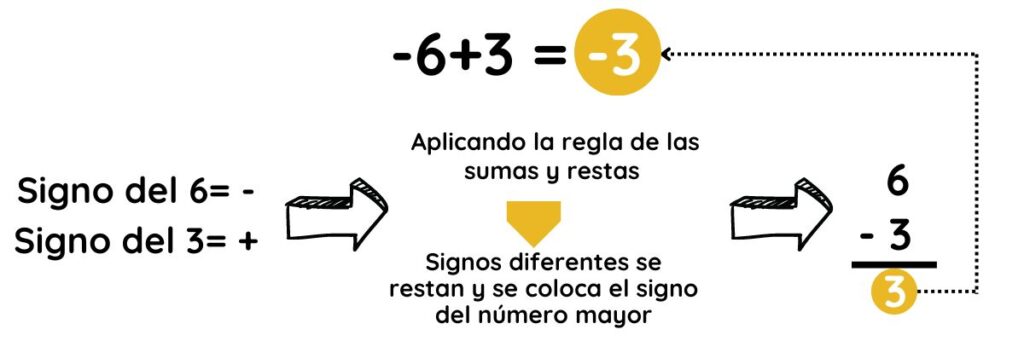
Fig.4. Ejemplos de aplicación de la regla de suma y resta
▶︎ PROPIEDADES
La suma de los números enteros cumple las siguientes propiedades:
a) CONMUTATIVA:
Esta propiedad establece: «El orden de los sumandos no altera la suma», representándose como :
a+b = b+a
A continuación un ejemplo gráfico de la propiedad:
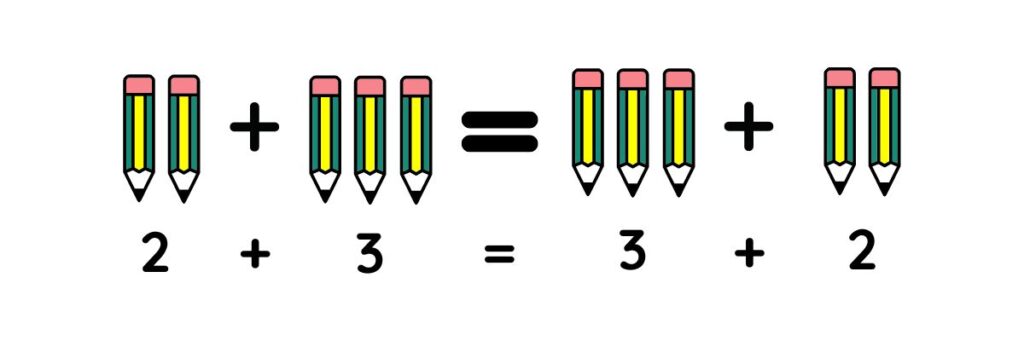
b) ASOCIATIVA:
Esta propiedad establece: «La forma en que se agrupan los sumandos no altera la suma» y se representa como:
(a+b)+c= a+(b+c)
A continuación un ejemplo gráfico de la propiedad:
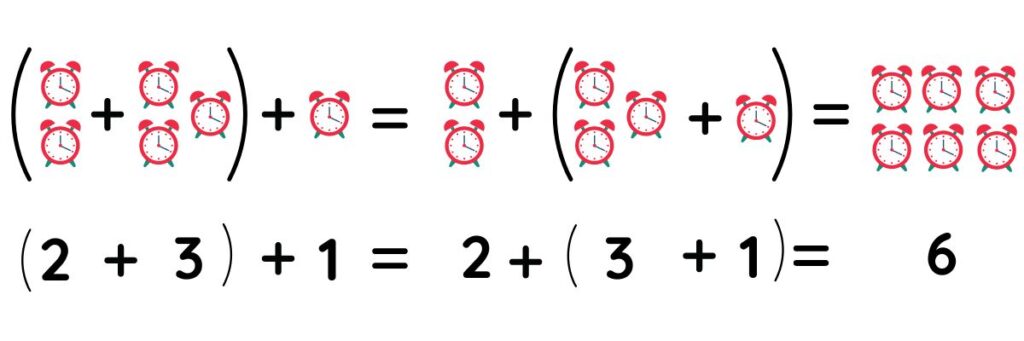
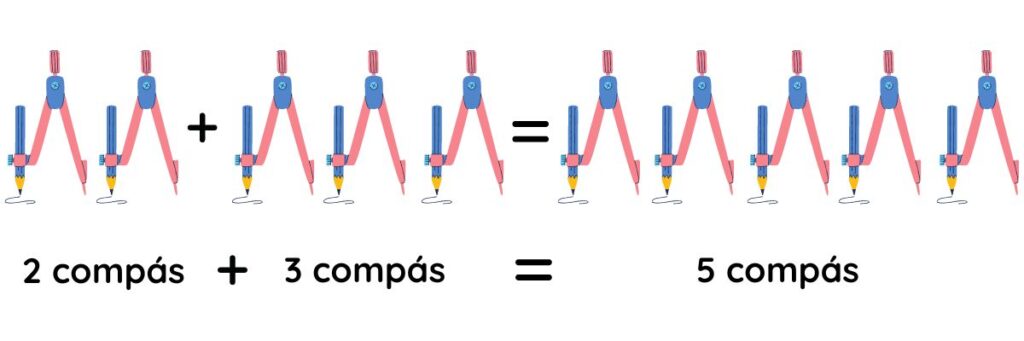
c) CLAUSURA:
Esta propiedad establece: «Al sumar números enteros siempre resultará un número entero» y se representa como:
a ⋀ b ∈ ℤ ⇒ a + b ∈ ℤ
A continuación un ejemplo gráfico de la propiedad:
d) ELEMENTO NEUTRO:
Es aquel número que, al ser operado con otro, da como resultado este último. En el caso de la adición es el cero y se representa como:
a + 0 = 0 + a = a
A continuación un ejemplo gráfico de la propiedad:
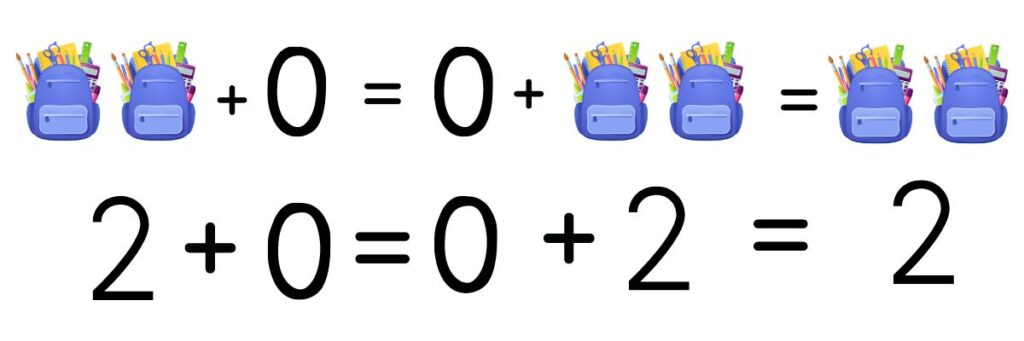
e) ELEMENTO OPUESTO O INVERSO ADITIVO:
Es aquel número que, al sumarse con otro, da como resultado el elemento neutro (cero). Además, un número y su inverso aditivo tienen el mismo valor absoluto y se representa:
a + (–a) = (–a) + a = 0
A continuación un ejemplo gráfico de la propiedad:
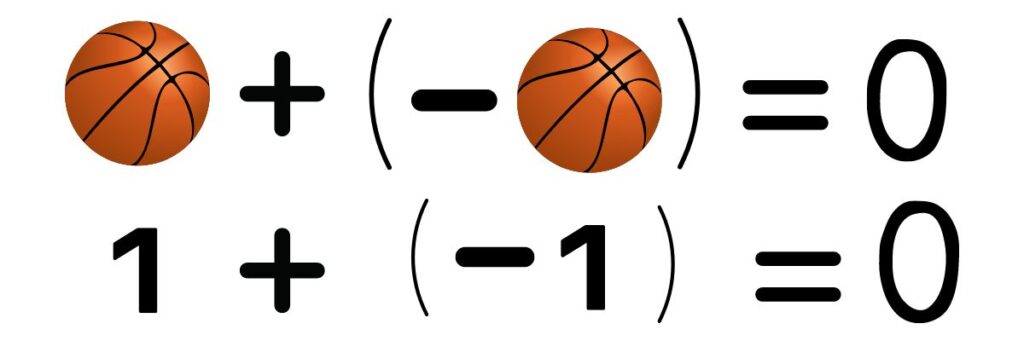
📌MULTIPLICACIÓN
La multiplicación de números enteros es una operación matemática que consiste en sumar un número (llamado multiplicando) un cierto número de veces, determinado por otro número (llamado multiplicador). Los números enteros incluyen números positivos, negativos y el cero.
▶︎ REGLA DE LOS SIGNOS
Para desarrollar una multiplicación, es necesario conocer la regla de los signos, la cual se presenta a continuación:

Ejemplos de aplicación de la regla:
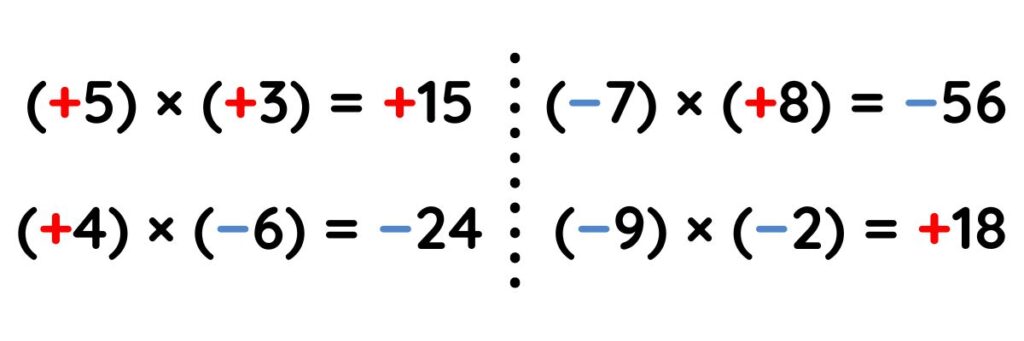
📌DIVISIÓN
La división de números enteros es una operación matemática en la que se distribuye un número (dividendo) en un cierto número de partes iguales, determinado por otro número (divisor). Los números enteros pueden ser positivos, negativos o cero.
▶︎ REGLA DE LOS SIGNOS
Para desarrollar una división, es necesario conocer la regla de los signos, la cual se presenta a continuación:

Ejemplos de aplicación de la regla:
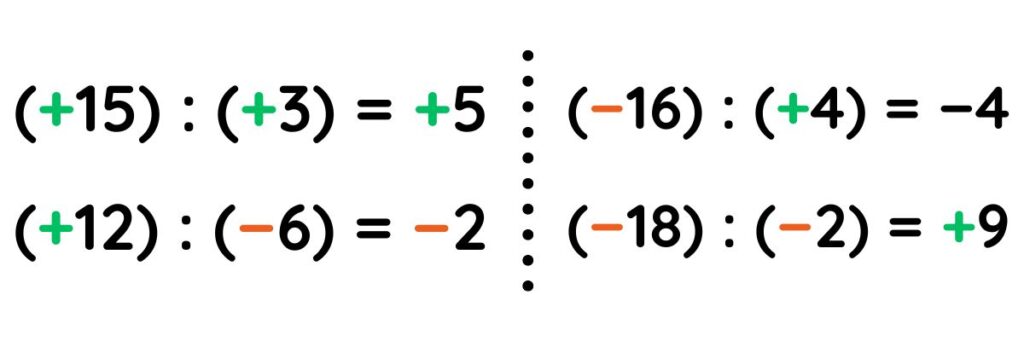
En esta sección, hemos explicado las principales características de los números enteros, con el objetivo de presentar de forma práctica y sencilla los pasos para resolver operaciones aritméticas como la suma, resta, multiplicación y división. En la siguiente publicación, mostraremos ejercicios resueltos y propuestos para la practica y reforzamiento de los conocimientos.


